Centripetal Force Formula
Any force, or combination of forces, can result in centripetal or radial acceleration. A few examples are the tension in the rope on a tether ball, the force of Earth's gravity on the Moon, friction between roller skates and a rink floor, the force of a banked highway on a car, and forces on the tube of a spinning centrifuge.
The term centripetal force refers to any net force that causes uniform circular motion. A centripetal force is directed towards the centre of curvature, just as a centripetal acceleration.
Formula of Centripetal Force
Centripetal force refers to a force that acts on a body travelling in a circular route and is directed towards the centre of the body. When an item moves along a circular direction at a constant speed, it feels an accelerating centripetal force towards the centre.
The equation for centripetal force is as follows.
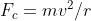
Where
Fc is the centripetal force
m is mass
v is velocity
r is the radius of the path
Solved Examples on Centripetal Force
Example 1: A van of 1,500 Kg is travelling at 30.0 m/s covers a curve of radius 300 m. Find the centripetal force.
Solution
The given parameters are
mass = 1,500 Kg
radius = 300 m
Velocity = 30.0 m/s
Substitute the values in the given formula
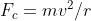
$$F_c= 1500(900)/300$$
$$F_c = 4500 N$$